
Материалы
Экономьте время на разработке,
используя свободные формы от Линко

Экономьте время на разработке,
используя свободные формы от Линко
Общество с ограниченной ответственностью "Линко", ИНН 7203563403, ERID: 2Vtzqv74E4X

|
Открытая разработка документов | Линко Open Source
Руководство по качеству лаборатории
Версия от 12.01.23
|
ВЕРНУТЬСЯ К ПЕРЕЧНЮ ДОКУМЕНТОВ ❯
ПЕРЕЙТИ К ТРЕБОВАНИЯМ ГОСТ 17025 ❯
7.6.2.1. Этап 1: Описание
Цель этого этапа – определить, что именно измеряется, включая соотношение между измеряемой величиной и параметрами (например, измеряемые величины, константы, значения эталонов для градуировки и т. д.).
Записывается математическая зависимость между входными и исходящей величинами (расчетная формула):
Y = f(X1, …, Xm)
(1)
где Y – измеряемая величина;
X1, …, Xm – входные величины (непосредственно измеряемые или другие величины, влияющие на результат измерения);
m – число этих величин;
f – вид функциональной зависимости.
Оценку измеряемой величины y вычисляют как функцию оценок входных величин x1, …, xm после внесения поправок на все известные источники неопределенности, имеющие систематический характер:
y = f(x1, …, xm)
(2)
7.6.2.2. Этап 2: Выявление источников неопределенности
Сначала идентифицируются источники неопределенности каждой входной величины. Такими источниками могут быть:
Источники выбираются таким образом, чтобы они были независимы. Рассчитывается вклад в стандартную неопределенность каждого источника.
7.6.2.3. Этап 3: Количественное описание составляющих неопределенности
Затем вычисляют стандартные неопределенности входных величин u(xi) (i = 1, … , m) и возможные коэффициенты корреляции r(xi, хj) оценок i-й и j-й входных величин (j = 1, …, m).
Различают два типа вычисления стандартной неопределенности:
Вычисление стандартной неопределенности по типу А – uA
Стандартную неопределенность единичного измерения i-й входной величины uA,iвычисляют по формуле:
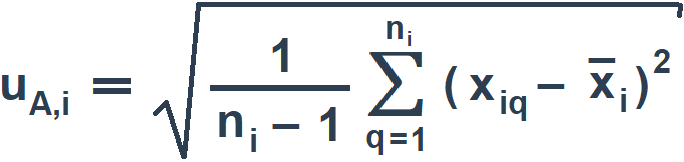
(3)
Стандартную неопределенность uA(хi) измерений i-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле:
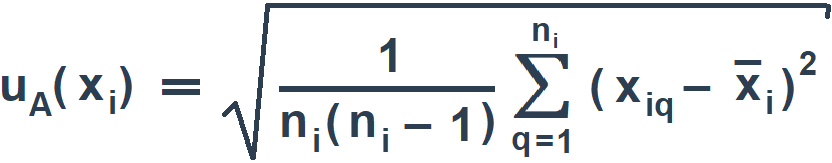
(4)
Вычисление стандартной неопределенности по типу В – uB
а) информацию нормативных документов (ГОСТ и ТУ на изделие, данные о методах и средствах измерений и испытаний, условия проведения испытаний, внешние воздействующие факторы и т. д.);
б) данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;
в) данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;
г) неопределенности констант и справочных данных;
д) данные поверки, калибровки, сведения изготовителя о приборе и т. п.
Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах [(bi-, bi+) для i-й входной величины]. При этом стандартную неопределенность, вычисляемую по типу В – uB(xi), определяют по формуле:
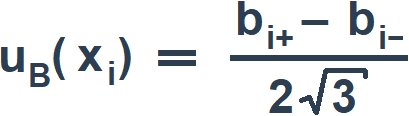
(5)
а для симметричных границ (±bi) – по формуле:
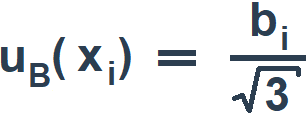
(6)
Для вычисления коэффициента корреляции r(xi, xj) используют согласованные пары измерений (xil, xjl) (где l = 1, …, nij; nij – число согласованных пар результатов измерений):
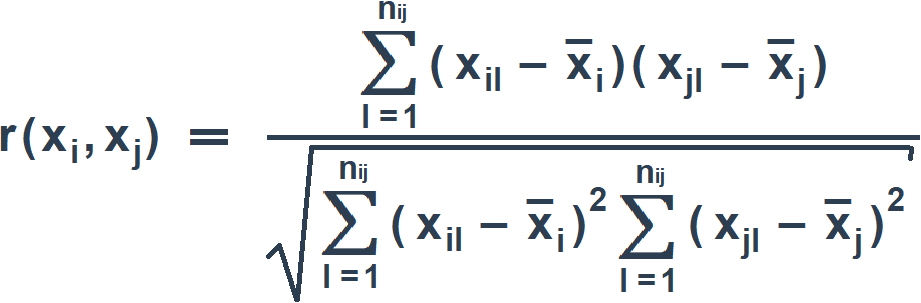
(7)
7.6.2.4. Этап 4: Вычисление суммарной стандартной неопределенности uc
В случае некоррелированных оценок x1, …, xm суммарную стандартную неопределенность uc(y) вычисляют по формуле:
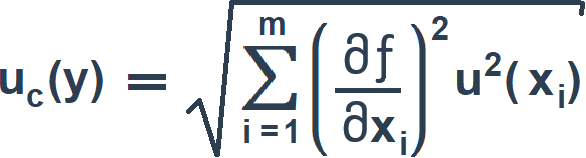
(8)
В случае коррелированных оценок x1, …, xmсуммарную стандартную неопределенность вычисляют по формуле:
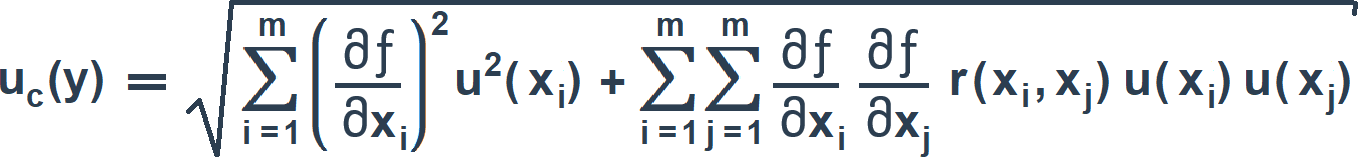
(9)
где r(xi, xj) – коэффициент корреляции;
u(xi) – стандартная неопределенность i-й входной величины, вычисленная по типу А или В.
7.6.2.5. Этап 5: Выбор коэффициента охвата k при вычислении расширенной неопределенности
Расширенная неопределенность вычисляется по формуле:
U = k × uc
(10)
где k – коэффициент охвата (числовой коэффициент, используемый как множитель при суммарной стандартной неопределенности для получения расширенной неопределенности).
В общем случае коэффициент охвата k выбирают в соответствии с формулой
k = tp(νeff)
(11)
где tp(νeff) – квантиль распределения Стьюдента с эффективным числом степеней свободы νeff и доверительной вероятностью (уровнем доверия) р. Значения коэффициента tp(νeff) приведены в Таблице 1.
Таблица 1 — Значения коэффициента tp(ν) для случайной величины, имеющей распределение Стьюдента с ν степенями свободы
| ν | tp(ν) | |
| p = 0,95 | p = 0,99 | |
| 3 | 3,182 | 5,841 |
| 4 | 2,776 | 4,604 |
| 5 | 2,571 | 4,032 |
| 6 | 2,447 | 3,707 |
| 7 | 2,365 | 3,499 |
| 8 | 2,306 | 3,355 |
| 9 | 2,262 | 3,250 |
| 10 | 2,228 | 3,169 |
| 12 | 2,179 | 3,055 |
| 14 | 2,145 | 2,977 |
| 16 | 2,120 | 2,921 |
| 18 | 2,101 | 2,878 |
| 20 | 2,086 | 2,845 |
| 22 | 2,074 | 2,819 |
| 24 | 2,064 | 2,797 |
| 26 | 2,056 | 2,779 |
| 28 | 2,048 | 2,763 |
| 30 | 2,042 | 2,750 |
| ∞ | 1,960 | 2,576 |
Эффективное число степеней свободы определяют по формуле:
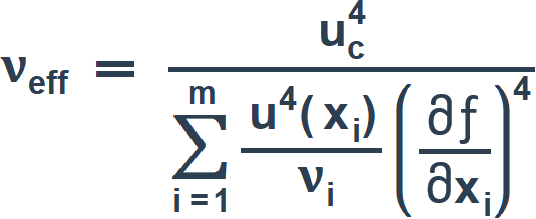
(12)
где vi– число степеней свободы при определении оценки i-й входной величины, при этом:
Во многих практических случаях при вычислении неопределенностей результатов измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины и полагают: k = 2 при р ≈ 0,95 и k = 3 при р ≈ 0,99.
При предположении о равномерности закона распределения полагают: k = 1,65 при р ≈ 0,95 и k = 1,71 при р ≈ 0,99.
Рекомендации по оформлению раздела «Оценивание неопределенности измерений»
Оценивание неопределенности (характеристик погрешности) результатов испытаний может проводиться по следующим документам:
Неопределенность результатов устанавливаются для всего диапазона действия методик.
При оценке неопределенности результатов анализа все составляющие неопределенности, являющиеся существенными в данной ситуации, принимаются во внимание при помощи соответствующих методов анализа.
Основными источниками неопределенности могут являться:
Документ создается сообществом лабораторий и открыт для дополнения и редактирования.
Вы можете участвовать в корректировке и дополнении, а также направить нам свою версию документа для включения её в состав данного материала. Для этой цели используйте форму загрузки внизу страницы.
Данный материал будет полезен для разработки документнов системы менеджмента своей лаборатории.
ВЕРНУТЬСЯ К ПЕРЕЧНЮ ДОКУМЕНТОВ ❯
ПЕРЕЙТИ К ТРЕБОВАНИЯМ ГОСТ 17025 ❯
Общество с ограниченной ответственностью «Винсер», ИНН 7733533010, ERID: 2VtzqvZQBRb

Общество с ограниченной ответственностью "Линко", ИНН 7203563403, ERID: 2VtzqvQuSFy
